ความสัมพันธ์และฟังก์ชัน

การเท่ากันของคู่อันดับ

บทนิยาม     คู่อันดับ  (a, b)  =  (c, d)   ก็ต่อเมื่อ   a  =  c  และ  b  =  d

เมื่อ  a, b, c, d  เป็นจำนวนจริงใด ๆ

ตัวอย่างที่  1    จากการเท่ากันของคู่อันดับต่อไปนี้จงหาค่าตัวแปร

1.1    (5, 9) = (a, 9)   จะได้        a =  5

1.2    (a, 7) = (-3, 7)  จะได้       a =  -3

1.3    (a+2, -1) = (8, -1) จะได้  a =  6

 ตัวอย่างที่  2         จงหาค่า  x  และ  y  ที่ทำให้  (x + 2, y + 10) 

       วิธีทำ       จากความหมายการเท่ากันของคู่อันดับ  จะได้ว่า

x + 2   =   6            และ      y + 10   =   12

\         x   =   4             และ             y   =   2

ตัวอย่างที่  3         จงหาค่าของ x  และ  y  ที่ทำให้  (2x + y, 24)  =  (6, 3x – y)

        วิธีทำ      จากความหมายการเท่ากันของคู่อันดับ  จะได้ว่า

2x + y              =             6              ………………………..    (1)

3x – y              =             24           ………………………..    (2)

(1) + (2) ;    5x     =             30

x     =             6

แทนค่า  x  ใน  (1)   จะได้

y            =             -6

ความสัมพันธ์

คู่อันดับ (Order Pair) เป็นการจับคู่สิ่งของโดยถือลำดับเป็นสำคัญ เช่น คู่อันดับ a, b จะเขียนแทนด้วย (a, b) เรียก a ว่าเป็นสมาชิกตัวหน้า และเรียก b ว่าเป็นสมาชิกตัวหลัง

(การเท่ากับของคู่อันดับ) (a, b) = (c, d) ก็ต่อเมื่อ a = c และ b = d

ผลคูณคาร์ทีเชียน (Cartesian Product) ผลคูณคาร์ทีเซียนของเซต A และเซต B คือ เซตของคู่อันดับ (a, b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B

สัญลักษณ์      ผลคูณคาร์ทีเซียนของเซต A และเซต B เขียนแทนด้วย A x B

หรือ เขียนในรูปเซตแบบบอกเงื่อนไขจะได้ว่า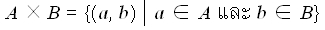 

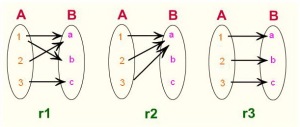
ความสัมพันธ์ (Relation)r เป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ A x B

โดเมน (Domain) และ เรนจ์ (พิสัย) (Range)

โดเมน (Domain) ของความสัมพันธ์ r คือ เซตที่มีสมาชิกตัวหน้าของทุกคู่อันดับในความสัมพันธ์ rใช้สัญลักษณ์แทนด้วย Dr ดังนั้น  Dr = {x | (x, y) ε r}

 เรนจ์ (Range) ของความสัมพันธ์ r คือ เซตที่มีสมาชิกตัวหลังของทุกคู่อันดับในความสัมพันธ์ r ใช้สัญลักษณ์แทนด้วย R rดังนั้น  Rr = {y | (x, y) ε r}

หลักเกณฑ์ในการพิจารณาหาโดเมนและเรนจ์ในความสัมพันธ์ R

ลักษณะของความสัมพันธ์	วิธีหาโดเมน	วิธีหาเรนจ์
เซตแบบแจกแจงสมาชิก	พิจารณาสมาชิกตัวหน้าของทุกคู่อันดับในความสัมพันธ์ r	พิจารณาสมาชิกตัวหลังของทุกคู่อันดับในความสัมพันธ์ r
เซตแบบบอกเงื่อนไข	1.      เปลี่ยนเป็นเซตแบบแจกแจงสมาชิกแล้วพิจารณาสมาชิกตัวหน้าของทุกคู่อันดับในความสัมพันธ์ r 2.      พิจารณารูปแบบของเงื่อนไขแล้วจัด y ให้อยู่ในรูป x แล้วหาค่า x ที่ทำให้ y เป็นจริงตามเงื่อนไข 3.      เปลี่ยนเป็นเซตแบบแจกแจงสมาชิกแล้วพิจารณาสมาชิกตัวหลังของทุกคู่อันดับในความสัมพันธ์ r 4.      พิจารณารูปแบบของเงื่อนไขแล้วจัด x ให้อยู่ในรูป y แล้วหาค่า y ที่ทำให้ x เป็นจริงตามเงื่อนไข
กราฟ	พิจารณาค่าของ x ทั้งหมดบนแกน X ที่ใช้ในการเขียนกราฟ	พิจารณาค่าของ y ทั้งหมดบนแกน Y ที่ใช้ในการเขียนกราฟ

ตัวผกผันของความสัมพันธ์ (Inverse of Relation) อินเวอร์สของความสัมพันธ์ r คือ ความสัมพันธ์ซึ่งเกิดจากการสลับที่ของสมาชิกตัวหน้าและสมาชิกตัวหลังในแต่ละคู่อันดับที่เป็นสมาชิกของ rเขียน 

r-1 ในรูปเซตแบบบอกเงื่อนไขได้ดังนี้  r-1 = {(x, y) | (y, x) ε r}

ถ้า r เป็นความสัมพันธ์จาก A ไป B แล้ว r-1 จะเป็นความสัมพันธ์จาก B ไป Aสัญลักษณ์         อินเวอร์สของความสัมพันธ์ r เขียนแทนด้วย r-1

ฟังก์ชัน

ฟังก์ชัน (Function)  คือ  ความสัมพันธ์  ซึ่งในสองคู่อันดับใด ๆ ของความสัมพันธ์นั้น  ถ้ามีสมาชิกตัวหน้าเท่ากันแล้ว  สมาชิกตัวหลังต้องไม่แตกต่างกันหรือ

ฟังก์ชัน  คือ  ความสัมพันธ์  ซึ่งในสองคู่อันดับใด ๆ ของความสัมพันธ์นั้น  ถ้าสมาชิกตัวหน้าเท่ากัน  สมาชิกตัวหลังต้องเท่ากันด้วย1)  ถ้าแต่ละค่าของ x หาค่า y ได้เพียงค่าเดียว  สรุปว่า r เป็นฟังก์ชัน2)  ถ้ามีบางค่าของ x ที่ทำให้หาค่า y ได้มากกว่าหนึ่งค่า  สรุปว่า r ไม่เป็นฟังก์ชันสมมติให้ (x, y) ε r และ (x, z) ε r  ดังนั้นจะได้เงื่อนไข  r(x, y)  และ  r(x, z) พิจารณา1)  ถ้าสามารถแสดงได้ว่า  y = z จะได้ว่า r เป็นฟังก์ชัน2)  ถ้ากรณีที่มี  y ε z  จะได้ว่า  r  ไม่เป็นฟังก์ชันกำหนดกราฟความสัมพันธ์ r ให้ลากเส้นตรงที่ขนานกับแกน Y และให้ตัดกราฟของความสัมพันธ์ rพิจารณา1)  ถ้าเส้นตรงแต่ละเส้นตัดกราฟของ r ได้เพียงจุดเดียวเท่านั้น จะได้ว่า r เป็นฟังก์ชัน2)  ถ้ามีเส้นตรงบางเส้นตัดกราฟของ r มากกว่าหนึ่งจุด  จะได้ว่า r จะไม่เป็นฟังก์ชันf จะเป็นฟังก์ชันจาก A ไป B (function from A to B) ก็ต่อเมื่อ1)    f เป็นฟังก์ชัน2)    Df = A3)    Rf  ε B1)    f เป็นฟังก์ชัน2)    Df = A3)    Rf = Bf : AB อ่านว่า f เป็นฟังก์ชันจาก A ไปทั่วถึง B

นั่นคือ   ความสัมพันธ์ f จะเป็นฟังก์ชัน ก็ต่อเมื่อ ถ้า (x, y1) ε f และ (x, y2) ε f แล้ว  y1 = y2

ถ้าหากว่าความสัมพันธ์ที่กำหนดให้อยู่ในรูปแบบบอกเงื่อนไข  การตรวจสอบว่าความสัมพันธ์นั้นเป็นฟังก์ชันหรือไม่สามารถทำได้กลายวิธี  ดังต่อไปนี้

วิธีที่  1      ถ้า  r  เป็นความสัมพันธ์ซึ่งประกอบด้วยคู่อันดับ  (x, y)  และมีเงื่อนไข  r(x, y)  แล้ว  ให้นำเงื่อนไข  r(x, y)  มาเขียนใหม่โดยเขียน y ในรูปของ x และพิจารณาดังนี้

วิธีที่  2      เมื่อกำหนดความสัมพันธ์ r ซึ่งประกอบด้วยคู่อันดับ (x, y) และมีเงื่อนไข  r(x, y)

วิธีที่  3       โดยใช้กราฟ

กำหนดให้ f เป็นฟังก์ชัน เรามีข้อตกลงเกี่ยวกับการเขียนสัญลักษณ์ ดังนี้

(x, y) ε R  จะเขียนแทนด้วย y = f(x)

เรียก f(x) ว่าค่าของฟังก์ชัน f  ที่ x หรือเรียกว่าภาพฉาย (image) ของ x ภายใต้ฟังก์ชัน f

อ่าน f(x) ว่า เอฟของเอ็กซ์ หรือ เอฟที่เอ็กซ์ หรือเรียกสั้นๆ ว่า เอฟเอ็กซ์

เราจะพบการใช้สัญลักษณ์เกี่ยวกับฟังก์ชันอยู่ 2 ลักษณะที่สำคัญคือ การเขียน f และ f(x) 

ความแตกต่างของการเขียนและการนำไปใช้

1) การเขียน f จะเป็นการกำหนดชื่อฟังก์ชัน (คล้ายการกำหนดชื่อเซต) เช่น กำหนดให้ f เป็นฟังก์ชัน เป็นต้น การเขียน f จะเขียนในรูปเซตแบบแจกแจงสมาชิก หรือว่าเซตแบบบอกเงื่อนไขก็ได้ เช่น          f = {(2, 5), (3, 7), (4, 9)} หรือ     f = {(x, y) | y = 2x + 1}  เป็นต้น

2) การเขียน f(x) จะเป็นการนิยามฟังก์ชัน f ว่ามีเงื่อนไข หรือลักษณะอย่างไร กำหนดให้เป็นอย่างไร มักเขียนในรูปนิพจน์ทางคณิตศาสตร์ (ประโยคสัญลักษณ์) แสดงความสัมพันธ์ตั้งแต่ 2 ตัวแปรขึ้นไป และมักเขียนในรูปสมการ เช่น f(x) = 2x + 1 หรือบางครั้งอาจเขียน y = 2x + 1 ให้เข้ใจว่า การนิยามฟังก์ชัน f จะเขียนให้อยู่ในรูป y = f(x)

ดังนั้น นักรเยนจะพบเสมอว่า ในโจทย์ปัญหาเกี่ยวกับฟังก์ชันโดยทั่วไป มักจะขึ้นต้นในทำนองว่า “กำหนดให้ f เป็นฟังก์ชันซึ่งนิยามว่า f(x) = …”  เป็นต้น

ดังนี้แล้ว พึงระลึกถึงและนำไปใช้ให้ถูกต้องด้วยความเคร่งครัดและระมัดระวังพีชคณิตของฟังก์ชัน หรือ การดำเนินการของฟังก์ชัน (Algebric Function or Operation of Function)ฟังก์ชันประกอบ หรือ ฟังก์ชันคอมโพสิต (Composite Function)

ตัวผกผันของฟังก์ชัน หรือ ฟังก์ชันอินเวอร์ส (Inverse of Function)ฟังก์ชันจากเซตหนึ่งไปยังอีกเซตหนึ่ง

กำหนดให้ A และ B เป็นเซต

สัญลักษณ์  f  เป็นฟังก์ชันจาก A ไป B จะเขียนแทนด้วย f : A → B  อ่านว่า f เป็นฟังก์ชันจาก Aไป B

ฟังก์ชันจาก A ไปทั่วถึง B

f จะเป็นฟังก์ชันจาก A ไปทั่วถึง B (function from A onto B) ก็เต่อเมื่อ

สัญลักษณ์   f เป็นฟังก์ชันจาก A ไป B จะเขียนแทนด้วย f : AB  หรือ ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B

ประเภทของฟังก์ชัน

ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไปทั่วถึง B

ฟังก์ชันเชิงเส้น (Linear Funtion)

ฟังก์ชันพหุนาม (Polynomial Function)

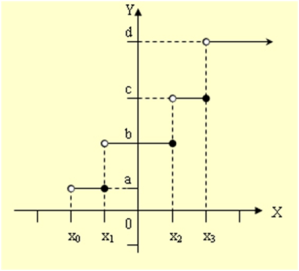
ฟังก์ชันขั้นบันได (Step Function)

ฟังก์ชันเอกซโพเนนเชียล (Exponential Function)

ฟังก์ชันลอการิทึม (Logarithm Function)

ฟังก์ชันตรีโกณมิติ (Trigonometry Function)

ฟังก์ชันค่าสัมบูรณ์ (Absolute Value Function)