ฟังก์ชันเอกซโพเนนเชียล&ลอการิทึม& คอมโพสิท

ฟังก์ชันเอกซโพเนนเชียล (Exponential Function)

ฟังก์ชันเอกโพเนนเชียล

จากการศึกษาในเรื่องเลขยกกำลัง  ซึ่งท้ายที่สุดเราได้สนใจเลขยกกำลังที่มีฐานเป็นจำนวนจริงบวก  และเลขชี้กำลังเป็นจำนวนจริงใด ๆ แต่ได้มีนักคณิตศาสตร์ได้สังเกตเห็นว่า  ถ้าเลขยกกำลังมีฐานเป็น 1  และเลขชี้กำลังเป็นจำนวนจริงใด ๆ ดังนี้   ถ้ากำหนดให้      a = 1  และ x เป็นจำนวนจริงใดแล้วจะได้   ax   =  1x   =  1

ข้อสังเกต  จากข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล

f(x) = 1x เป็นฟังก์ชันคงตัวเนื่องจาก 1x = 1  ดังนั้นในข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล  จึงไม่สนใจ  ฐาน (a) ที่เป็น 1

f(x) = 1x  ไม่เป็นฟังก์ชันเอ็กซ์โพเนนเชียล  เนื่องจาก  f(x) = 1x เป็นฟังก์ชันคงตัว

จากเงื่อนไขที่ว่า  y = ax, a > 0, a ¹ 1  ทำให้เราทราบได้เลยว่าฐาน (a) มีอยู่ 2 ลักษณะ คือ  0 < a < 1 กับ a > 1

ฟังก์ชันเอกซ์โพเนนเชียลจะมีอยู่ 2 ชนิด  โดยขึ้นอยู่กับลักษณะของฐาน (a)  ดังนี้

ชนิดที่ 1     y = ax, 0 < a < 1

ชนิดที่ 2     y = ax, a > 1

กราฟของสมการ y = ax ในฐาน a ต่าง ๆ : ฐาน 10 (สีเขียว), ฐาน e (สีแดง), ฐาน 2 (สีน้ำเงิน), และฐาน ½ (สีฟ้า) เส้นโค้งแต่ละเส้นผ่านจุด (0, 1) เนื่องจากจำนวนที่ไม่เป็นศูนย์ใด ๆ ยกกำลัง 0 จะได้ 1 และที่ x = 1 ค่าของ y จะเท่ากับฐาน เนื่องจากจำนวนใด ๆ ยกกำลัง 1 จะได้จำนวนเดิม

ฟังก์ชันลอการิทึม (Logarithm Function)

ลอการิทึม (อังกฤษ: logarithm) เป็นการดำเนินการทางคณิตศาสตร์ที่เป็นฟังก์ชันผกผันของฟังก์ชันเลขชี้กำลัง ค่าลอการิทึมของจำนวนหนึ่งโดยกำหนดฐานไว้ให้ จะมีค่าเทียบเท่ากับ การเอาฐานมายกกำลังค่าลอการิทึม ซึ่งจะให้คำตอบเป็นจำนวนนั้น ตัวอย่างเช่น

• ลอการิทึมของ 1000 ในฐาน 10 มีค่าเป็น 3 เพราะว่า 10 คูณกัน 3 ตัวแล้วได้ 1000 นั่นคือ 10 × 10 × 10 = 1000
• ลอการิทึมของ 32 ในฐาน 2 มีค่าเป็น 5 เพราะว่า 2 คูณกัน 5 ตัวแล้วได้ 32 นั่นคือ 2 × 2 × 2 × 2 × 2 = 32

ถ้าเขียนด้วยสัญลักษณ์ยกกำลังจะได้ว่า

• 10³ = 1000 ดังนั้น log₁₀ 1000 = 3
• 2⁵ = 32 ดังนั้น log₂ 32 = 5

ลอการิทึมของ x ในฐาน b เขียนแทนด้วย log_b x หรือถ้าฐานมีค่าใด ๆ เป็นปริยาย จะเขียนเพียงแค่ log x (ไม่จำเป็นต้องใส่วงเล็บรอบ x) ดังนั้นสำหรับจำนวน x ฐาน b และเลขชี้กำลัง y ที่สามารถเป็นไปได้

${\displaystyle x=b^{y}\,\Rightarrow \,y=\log _{b}x\!}$

คุณลักษณะหนึ่งที่สำคัญของลอการิทึมคือการลดทอนการคูณไปเป็นการบวกดังนี้

${\displaystyle \log xy=\log x+\log y\!}$

หมายความว่า ลอการิทึมของผลคูณของสองจำนวน จะเท่ากับผลรวมของลอการิทึมของแต่ละจำนวน การใช้ลอการิทึมเพื่อลดทอนการคำนวณที่ซับซ้อนเป็นหนึ่งในแรงผลักดันอย่างมีนัยสำคัญในการพัฒนาที่มีมาแต่เดิม มีการใช้งานลอการิทึมอย่างกว้างขวางทั้งในงานสถิติศาสตร์ เคมี ฟิสิกส์ ดาราศาสตร์ วิทยาการคอมพิวเตอร์ เศรษฐศาสตร์ ดนตรี และวิศวกรรมศาสตร์

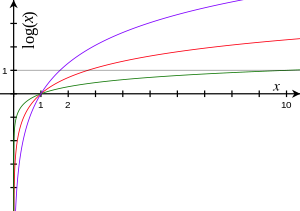กราฟของฟังก์ชันลอการิทึมในฐานต่าง ๆ สีแดงคือฐาน e สีเขียวคือฐาน 10 สีม่วงคือฐาน 1.7 กราฟทุกเส้นผ่านจุด (1, 0) เนื่องจากจำนวนใด ๆ ที่ไม่เป็นศูนย์ เมื่อยกกำลัง 0 แล้วได้ 1 และกราฟทุกเส้นผ่านจุด (b, 1) สำหรับฐาน b เพราะว่าจำนวนใด ๆ ยกกำลัง 1 แล้วได้ค่าเดิม เส้นโค้งทางซ้ายเข้าใกล้แกน y แต่ไม่ตัดกับแกน y เพราะมีภาวะเอกฐานอยู่ที่ x = 0 (เส้นกำกับในแนวดิ่ง)

ฟังก์ชันคอมโพสิท(Composite  Function)

    ฟังก์ชันคอมโพสิท (Composite  Function)

            เป็นการกระทำกันระหว่างฟังก์ชันตั้งแต่ 2 ฟังก์ชันขึ้นไปให้  f และ g  เป็นฟังก์ชัน  สำหรับฟังก์ชันที่เป็นเซตแบบแจกแจงเช่น

   f = {(1,3),(2,4),(3,5)}

   g = {(5,1),(3,2),(4,3)}

เราสามารถสร้างฟังก์ชันขึ้นมาใหม่ เรียกว่า gof (จีโอเอฟ) แต่ผมมักจะเรียกไปเลยว่า ก็อฟ (gof)  เป็นฟังก์ชันจาก f ไปยัง g

  จะได้       gof  = {(1,2),(2,4),(3,1)}

          (gof)(1) = g(f(1)) = g(3) = 2

          (gof)(2) = g(f(2)) = g(4) = 3

          (gof)(3) = g(f(3)) = g(5) = 1

นิยาม ให้ f และ g เป็นฟังก์ชัน และ R f ∩ Dg    ฟังก์ชันคอมโพสิทของ f และ g เขียนแทนด้วย gof  กำหนด (gof)(x) = g(f(x))  ซึ่ง f(x) ∈ Dg

ตัวอย่างที่ 1  กำหนด f = {(1,2),(3,4),(5,6),(7,8)}

                 g = {(2,a),(4,b),(7,c),(8,d)}

 จงหา (gof)(1) , (gof)(3) , (gof)(7)  พร้อมทั้งหา gof และ  fog

วิธีทำ   gof เป็นฟังก์ชัน จาก f ไป g

        R f   = {2,4,6,8} ,  Dg = {2,4,7,8}

        R f ∩ Dg  = {2,4,8}  ≠ Ø แสดงว่าหา gof ได้

    (gof)(1) = g(f(1)) = g(2) = a

    (gof)(3) = g(f(3)) = g(4) = b

    (gof)(7) = g(f(7)) = g(8) = d

  ดังนั้นจะได้  gof = {(1,a),(3,b),(7,d)}  fog  เป็นฟังก์ชันจาก g ไป f

      Rg  =  {a,b,c,d} ,  Df  =   {1,3,5,7}

      Rg  ∩  Df   = Ø  แสดงว่าหา fog   ไม่ได้

ตัวอย่างที่ 2  กำหนดให้ f(x) = 3x-5 , g(x) = 1/x-3

 จงหา  gof , fog , (gof)(3) , (fog)(2)

วิธีทำ

 1.) หา gof       R f  =  R       

                         Dg   =  R - {3}

     R f ∩ Dg  ≠ Ø แสดงว่าหา gof ได้    (gof)(x)  = g(f(x))

                                                                                = g(3x-5)

                                                                                =  1/(3x-5)-3  = 1/3x-8

  ดังนั้น gof = {(x,y) | y = 1/3x-8}  (gof)(3) = g(f(3)) = g(4) = 1

 2.)  หา  fog     Rg  ≠  0

                         Df  =  R

 

     
 3.)  Rg  ∩  Df   ≠ Ø  แสดงว่าหา fog ได้   
  (fog)(x)  = f(g(x)) = f(1/x-3)

                                                                                = 3(1/x-3)-5 = (3/x-3)-5

  (fog)(x)  = 18-5x/x-3

                                                                      fog       = {(x,y) |  y = 18-5x/x-3} 

                                                                 (fog)(2)   = 18-5(2)/2-3 = 18-10/-1

                                                                                = -8