กราฟของฟังก์ชัน f (อังกฤษ: graph of a function) ในทางคณิตศาสตร์ คือการรวบรวมคู่อันดับ (x, f(x)) ทั้งหมด ถ้าฟังก์ชันรับค่า x เป็นสเกลาร์
กราฟนี้จะเป็นกราฟสองมิติ และจะกลายเป็นเส้นโค้งสำหรับฟังก์ชันต่อเนื่อง
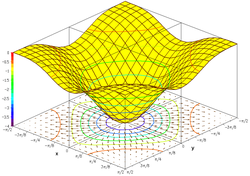
ถ้าฟังก์ชันรับค่า x เป็นคู่อันดับของจำนวนจริง (x1, x2) กราฟนี้จะเป็นการรวบรวมสามสิ่งอันดับ (x1, x2,
f(x1, x2)) ทั้งหมด
หรือเป็นกราฟสามมิติ และจะกลายเป็นพื้นผิวสำหรับฟังก์ชันต่อเนื่อง
หากกล่าวอย่างไม่เป็นทางการ ถ้า x เป็นจำนวนจริง และ f เป็นฟังก์ชันค่าจริง
กราฟ อาจหมายถึงตัวแทนเชิงภาพ (graphical representation) ของการรวบรวมเหล่านี้ในรูปแบบกราฟเส้น
นั่นคือเส้นโค้งบนระนาบคาร์ทีเซียน และแกนคาร์ทีเซียนเป็นต้น
การวาดกราฟบนระนาบคาร์ทีเซียนบางครั้งก็อาจเรียกว่า การร่างเส้นโค้ง (curve sketching) กราฟของฟังก์ชันจำนวนจริงอาจลงจุดได้โดยตรงบนตัวแทนเชิงภาพของฟังก์ชันนั้น
สำหรับฟังก์ชันทั่วไป ตัวแทนเชิงภาพไม่จำเป็นว่าจะต้องสามารถหาได้
และนิยามของกราฟของฟังก์ชันก็เพียงพอต่อความต้องการในประโยคคณิตศาสตร์ต่าง ๆ แล้ว
ตัวอย่างเช่น ทฤษฎีบทกราฟปิด (closed graph theorem) ในการวิเคราะห์เชิงฟังก์ชัน
มโนทัศน์ของกราฟของฟังก์ชันสามารถวางนัยทั่วไปเป็นกราฟของความสัมพันธ์
(graph of a relation) สังเกตว่าถึงแม้ฟังก์ชันหนึ่ง ๆ สามารถระบุได้ด้วยกราฟของมันเสมอ
แต่ฟังก์ชันสองฟังก์ชันที่มีโคโดเมนต่างกันก็อาจมีกราฟเหมือนกันได้
ฟังก์ชันเหล่านั้นจึงไม่ใช่ฟังก์ชันเดียวกัน ยกตัวอย่าง ฟังก์ชันพหุนามกำลังสามในตัวอย่างเป็นฟังก์ชันทั่วถึง
(surjection) ถ้าโคโดเมนเป็นจำนวนจริง
แต่จะไม่ใช่ฟังก์ชันทั่วถึงถ้าโคโดเมนเป็นจำนวนเชิงซ้อน
การทดสอบว่ากราฟเส้นโค้งหนึ่ง ๆ เป็นฟังก์ชันของ x หรือไม่ ให้ใช้การทดสอบเส้นแนวยืน (vertical line test) ในทางกลับกัน การทดสอบว่ากราฟเส้นโค้งหนึ่ง ๆ เป็นฟังก์ชันของ y หรือไม่ ให้ใช้การทดสอบเส้นแนวนอน (horizonal line test) ถ้าฟังก์ชันนั้นมีฟังก์ชันผกผัน
กราฟของฟังก์ชันผกผันจะหาได้จากเงาสะท้อนในกระจกของกราฟของฟังก์ชันเดิม
โดยมีเส้นตรง y = x เป็นแกน
ในทางวิทยาศาสตร์ วิศวกรรมศาสตร์ เทคโนโลยี การเงิน
และอื่น ๆ กราฟถูกใช้เป็นเครื่องมืออเนกประสงค์ กรณีง่ายสุดคือตัวแปรหนึ่ง ๆ
จะถูกลงจุด (plot) เป็นฟังก์ชันของตัวแปรอื่น โดยใช้แกนที่ตัดกันเป็นมุมฉากตามปกติ
ในรากฐานของคณิตศาสตร์สมัยใหม่อันเป็นที่รู้จักกันว่าทฤษฎีเซต
ฟังก์ชันและกราฟของฟังก์ชันโดยพื้นฐานถือว่าคือสิ่งเดียวกัน
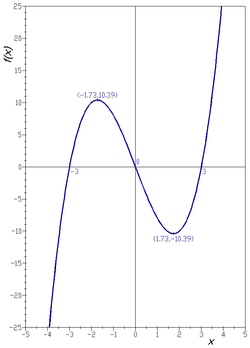
 กราฟของฟังก์ชัน
กราฟของฟังก์ชัน
ไม่มีความคิดเห็น:
แสดงความคิดเห็น